Como ya hemos estudiado en diédrico, al hablar de secciones nos referimos al corte que produce un plano en un poliedro.
En general lo que vamos a realizar, para hallar la sección, es intersección entre planos o entre recta y plano.
De partida, decir que si tenemos planos paralelos en el poliedro el corte en ambos serán rectas paralelas.
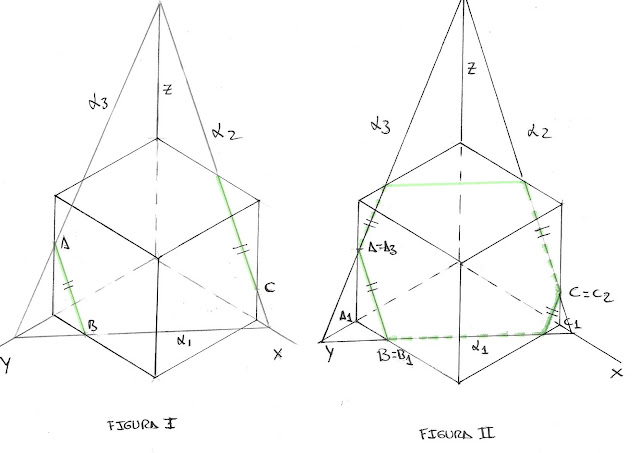
Ejemplo1: Figura 1 y 2.
Partimos de un cubo en isométrica y de tres puntos, A,B y C. Nos piden hallar la sección producida en el cubo por el plano que pasa por los tres puntos.
1º Si tengo dos puntos en una misma cara, la recta que forman pertenece a la sección.
2º La sección producida en la cara paralela a la anterior es una recta paralela. Esta última recta se encuentra en una cara del cubo pero también en el plano xoz luego está sobre la traza a2 del plano que secciona al cubo.
Una vez que tenemos una traza es fácil hallara las otras dos que pasan por A y por B. Recordamos que las trazas del plano se juntan dos a dos sobre los ejes.
3º Como el cubo está pegado a los planos de proyección es sencillo terminar la sección.
Sección del plano sobre el cubo.
1º Uno A y B y hallo la traza de la recta que forman con el xoy.
2º La traza anterior la uno con C y obtengo la traza a1 del plano sección.
3º La traza sobre el plano xoz tiene que pasar por el punto 1(donde se juntan las trazas del plano) y es paralela a la recta AB.
4º La traza sobre el plano yoz pasa por el punto 2 y por B.
5º completamos la sección en cada cara.
Video selectividad 2009
Cálculo de la sección producida por un plano en una pirámide en sistema isométrico. - (Modelo 2018 Madrid) - Selectividad PAU
https://youtu.be/BYuQ7e4N10U
https://www.mongge.com/ejercicios/25375
Sección de un plano en un poliedro: Modelo selectividad 2010.
https://www.mongge.com/ejercicios/25310
https://www.mongge.com/ejercicios/25307
Definir el plano ABC y determinar la sección que produce sobre la pieza representada en perspectiva isométrica.





No hay comentarios:
Publicar un comentario